Neste texto, o objetivo é apresentar brevemente algumas noções intuitivas à respeito de curvas associadas à um sólido geométrico bastante conhecido, o cone. Foi feita uma abordagem em relação às propriedades de reflexão que possibilitam uma série de aplicações as quais foram exemplificadas.
Primeiramente, define-se cone como sendo um sólido de revolução (“giro”) formado pela rotação de 360° em volta de um dos lados de um triângulo.
 |
| Figura 1: Revolução de triângulos. Fonte: UFF. |
Os cones podem ser classificados em simples e de duas folhas, conforme as figuras 1 e 2 , respectivamente:
 |
| Figura 2: Cone simples. |
 |
| Figura 3: Cone de duas folhas. |
 |
| Figura 4: Apolônio de Pérgamo. |
Historicamente, o estudo sistemático das cônicas ou das seções cônicas foi realizado sobretudo por um geômetra grego chamado Apolônio de Pergamo (cidade natal). Ele registrou seus estudos numa obra composta por 8 volumes chamada “Seções Cônicas”, sendo que 7 volumes chegaram até os tempos modernos. Os estudos das cônicas já eram realizados antes de Apolônio por outros geômetras da Antiguidade, como Menecmo, Euclides e Arquimedes. Entretanto, a obra de Apolônio foi a mais completa e aprofundada e, além disso, ele conseguiu gerar todas as cônicas de um único cone de duas folhas, simplesmente variando o plano de interseção.
A importância da contribuição da obra de Apolônio está na sua influência nos estudos astronômicos e geográficos de Ptolomeu, nas aplicações de ótica, de construção de espelhos, e estudo das órbitas planetárias de Kepler, nos estudos sobre a trajetória de projéteis de Galileu. Mais tarde, matemáticos como Isaac Newton e Fermat também fizeram uso, mesmo que indiretamente, dos estudos deixados por Apolônio.
A Circunferência
É uma curva plana fechada que se obtém quando um plano intercepta um cone reto e é paralelo à base desse cone. A circunferência possui características não comumente encontradas em outras figuras planas, como o fato de ser a única figura plana que pode ser rodada em torno de um ponto sem modificar sua posição aparente. É também a única figura que é simétrica em relação a um número infinito de eixos de simetria.
 |
| Figura 5: Corte de um cone por um plano paralelo à base. Fonte: mat.uel |
Também pode-se definir a circunferência como sendo o conjunto de pontos que estão à uma mesma distância de um ponto fixo. Essa distância é o raio e o ponto fixo é o centro da circunferência.
O estudo das circunferências, de seus elementos como o perímetro e a área, e outras relações envolvendo essas curvas tem sua importância dada grande variedade de itens com essa forma presentes em nosso dia. Um exemplo imediato é a roda que devido ao fato de ter essa forma circular, a ação da força de atrito com o solo é minimizada, facilitando o deslocamento de grandes massas.
A elipse
É uma curva plana fechada que se obtém quando um plano intercepta um cone reto de maneira inclinada em relação à sua base, sendo que essa inclinação deve ser menor do que a inclinação da geratriz do cone. Na elipse há a presença de dois pontos fixos, denominados focos e a soma das distâncias de qualquer ponto da elipse até esses focos sempre é um valor constante.
 |
| Figura 6: Corte de um cone por um plano não paralelo à base, mas com inclinação menor que a da geratriz. |
 |
| Figura 7: Propriedade da elipse. |
Uma propriedade muito importante da elipse é que qualquer raio luminoso ou onda sonora que saia de um dos focos será refletido pela elipse na direção do outro foco, conforme indicado na figura ao lado:
A propriedade acima justifica algumas aplicações da elipse como, por exemplo, a aplicação óptica de um dispositivo de iluminação usado em consultórios odontológicos. Este dispositivo consiste num espelho com a forma de um arco de elipse e numa lâmpada que se coloca no foco mais próximo. A luz da lâmpada é concentrada pelo espelho no outro foco, ajustando-se o dispositivo de forma a iluminar o ponto desejado.
 |
| Figura 8: Litotriptor com espelho elipsoidal. |
Ainda no campo da saúde, existe um procedimento muito utilizado no tratamento de cálculo renal, denominado litotripsia extracorpórea. Neste procedimento, conforme esquema abaixo, ondas de choque criadas fora do corpo do paciente viajam através da pele e tecidos até encontrarem os cálculos mais densos, pulverizando-os. O litotriptor possui um espelho elíptico que concentra os raios emitidos num determinado ponto com grande precisão.
Outra aplicação da propriedade acima é no campo da acústica utilizada em igrejas, auditórios e teatros, pois quando duas pessoas estão cada uma em um dos focos de um elipsóide (sólido que se obtém rodando uma elipse em torno do seu eixo, isto é, da reta definida pelos dois focos) e uma delas falar, mesmo que seja baixo, a outra pessoa ouvirá perfeitamente, mesmo que haja outros ruídos e sem que demais pessoas que estiverem entre os dois focos possam ouvir. Esses espaços são chamados de sala dos murmúrios ou sala dos sussurros e são utilizados em vários edifícios públicos da Europa e dos Estados Unidos.
Na arquitetura e engenharia há uma grande variedade de aplicações como no famoso Coliseu de Roma e em outras construções de pontes, arcos e cúpulas de igrejas.
 |
| Figura 9: Johannes Kepler. |
Outra aplicação da elipse foi nos estudos de Kepler na área de Astronomia. Ele formulou três leis a respeito dos movimentos planetários, sendo que a primeira dessas leis afirma que os planetas descrevem órbitas elípticas com o Sol ocupando um dos focos.
A parábola
É uma curva plana aberta que se obtém quando um plano intercepta um cone reto de modo paralelo à sua geratriz. Na parábola, todos os pontos estão a uma mesma distância de um ponto fixo, denominado foco, e de uma reta fixa, chamada diretriz.

 A propriedade de destaque na parábola, denominada de propriedade de reflexão, é o fato de que todo raio luminoso ou onda sonora que incida sobre a parábola paralelamente ao seu eixo é refletido de modo a passar pelo foco da parábola. O processo inverso também acontece, ou seja, qualquer raio ou onda que seja emitido do foco da parábola e que incida sobre a parábola é refletido numa mesma direção segundo retas paralelas ao eixo da parábola. Essa propriedade faz com que a parábola apresente várias aplicações, como por exemplo, em antenas parabólicas, faróis de veículos, fornos solares e em telescópios.
A propriedade de destaque na parábola, denominada de propriedade de reflexão, é o fato de que todo raio luminoso ou onda sonora que incida sobre a parábola paralelamente ao seu eixo é refletido de modo a passar pelo foco da parábola. O processo inverso também acontece, ou seja, qualquer raio ou onda que seja emitido do foco da parábola e que incida sobre a parábola é refletido numa mesma direção segundo retas paralelas ao eixo da parábola. Essa propriedade faz com que a parábola apresente várias aplicações, como por exemplo, em antenas parabólicas, faróis de veículos, fornos solares e em telescópios.
Em particular, no caso dos fornos ou coletores solares os raios de luz ao encontrarem um espelho parabólico convergem para o foco do espelho, onde a temperatura pode chegar a 3.500°C e neste ponto é colocado um dispositivo que irá utilizar a energia concentrada. Essa energia pode ser usada para gerar eletricidade, derretimento de aço, fazer combustível de hidrogênio ou nanomateriais. A seguir, a imagem do maior forno solar do mundo, situado na França.
Na engenharia, as pontes suspensas (juntamente com as pontes estaiadas) são bastante utilizadas, pois possibilitam os maiores vãos. Nessas pontes, a base (tabuleiro) é sustentada por vários cabos metálicos verticais (pendurais) ligados a dois cabos maiores principais, que por sua vez, são conectados às torres de sustentação. Os cabos comprimem as torres de sustentação e estas últimas transferem as forças de compressão para as fundações. Como os cabos verticais são distribuídos de maneira regular, a carga da ponte é distribuída de modo uniforme aos cabos principais, que formam uma parábola.
Como exemplos, apresenta-se a seguir a maior ponte suspensa do mundo, que fica no Japão, com extensão de quase 4 Km e vão central de quase 2 Km. Outra ponte suspensa, conhecida no Brasil, é a Ponte Hercílio Luz, que fica em Florianópolis, SC.
Vale a pena ressaltar que a parábola é também o gráfico que representa qualquer função do tipo f(x) = ax2 + bx + c, com a, b, c sendo números reais. Essa função é conhecida como função quadrática ou de 2.° grau.
A Hipérbole
É uma curva aberta, com dois ramos, que se obtém quando um plano intercepta um cone reto de modo perpendicular à base do cone, sendo que o ângulo do plano é maior do que o ângulo da geratriz do cone. Na hipérbole há a presença de dois pontos fixos, denominados focos, tal que a diferença entre as distâncias de qualquer ponto da hipérbole aos focos é sempre um valor constante.
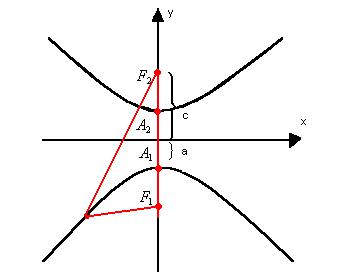
A propriedade de reflexão da hipérbole afirma que qualquer segmento de reta dirigido a um dos focos da hipérbole encontra o ramo correspondente e é refletido em direção ao outro foco.
Essa propriedade é muito aplicada nos telescópios de reflexão, os quais são constituídos de dois espelhos, sendo um maior, que é parabólico e outro menor, que é hiperbólico. Esses dois espelhos dispõem-se de modo que os eixos da parábola e da hipérbole coincidam e que o foco da parábola coincida com um dos focos da hipérbole, conforme esquema abaixo:
Nesse tipo de telescópio, quando os raios de luz se refletem no espelho parabólico são dirigidos para o foco, pela propriedade de reflexão da parábola. Como este também é foco da hipérbole, pela propriedade de reflexão desta os raios de luz refletem-se no espelho hiperbólico e seguem em direção ao outro foco da hipérbole. Os raios de luz passam através de um orifício no centro do espelho primário, atrás do qual está uma lente-ocular que permite corrigir ligeiramente a trajetória da luz, que chega finalmente aos olhos do observador ou à película fotográfica. A vantagem deste tipo de telescópio reside no fato de ter um comprimento muito menor do que os telescópios de refração (isto é, de lentes) com o mesmo poder de ampliação.
As curvas hiperbólicas também são utilizadas na arquitetura como pode ser observado da catedral de Brasília e no planetário do St. Louis Science Center, nos Estados Unidos.
 Já na engenharia civil, o hiperbolóide (sólido originado da rotação de uma hipérbole) é utilizado na construção de torres de refrigeração de usinas nucleares. Isso se deve ao fato de que o hiperbolóide é uma superfície duplamente regrada, ou seja, para cada um dos seus pontos existem duas retas distintas que se interceptam na superfície (observe detalhe na imagem da próxima página). Deste modo as torres podem ser construídas com vigas de aço retas, permitindo assim uma minimização dos ventos transversais e mantendo a integridade estrutural com uma utilização mínima de materiais de construção.
Já na engenharia civil, o hiperbolóide (sólido originado da rotação de uma hipérbole) é utilizado na construção de torres de refrigeração de usinas nucleares. Isso se deve ao fato de que o hiperbolóide é uma superfície duplamente regrada, ou seja, para cada um dos seus pontos existem duas retas distintas que se interceptam na superfície (observe detalhe na imagem da próxima página). Deste modo as torres podem ser construídas com vigas de aço retas, permitindo assim uma minimização dos ventos transversais e mantendo a integridade estrutural com uma utilização mínima de materiais de construção.
Finalmente, outra importante utilização das hipérboles é no sistema de localização em navegação, denominado de LORAN (Long Range Navigation - Navegação de Longa Distância). Este sistema permite a um navegante de um navio ou o piloto de um avião achar sua posição sem confiar em marcos visíveis. O LORAN utiliza hipérboles confocais, isto é, hipérboles com um dos focos em comum, onde estão os radares que emitem sinais. Cada par de radares dá uma hipérbole que contem a posição do navio ou do avião e, assim, a sua posição exata é o ponto onde as três hipérboles interceptam-se. Essa posição pode ser determinada pela plotagem das três hipérboles em um mapa, obtendo a interseção em comum usando coordenadas e computando algebricamente a interseção.










4 Comentários
Muito bom
ResponderExcluirBom mesmo
ResponderExcluirruim kkk
ResponderExcluirto brincando só poderia ter mais imagens explicando o assunto melhor, tipo como elas podem ser aplicadas na arquitetura e tal...
ResponderExcluir